プログラムには基調講演と書いてありますが、基調講演が何なのか私には分かりません。この会議の基調講演として何を取り上げるべきか、あるいはそのようなことを示唆するつもりは全くありません。私には私自身が言いたいこと、話したいことがあり、誰かが同じこと、あるいは似たようなことを話さなければならないと示唆するつもりは全くありません。ですから、私がお話ししたいのは、マイク・ダートゥーゾス氏が誰も話そうとしなかったと示唆したことです。コンピューターによる物理シミュレーションの問題についてお話ししたいと思います。具体的な方法についてお話ししたいと思います。それをこれから説明します。この話をする理由は、エド・フレドキン氏から学んだことであり、このテーマへの私の関心はすべて彼に触発されたものです。コンピューターの可能性、そして物理学の可能性について学ぶことが、私の目的です。もし私たちがすべての物理法則を完璧に理解していると仮定するなら、もちろんコンピュータに注意を払う必要はありません。物理法則について何か学ぶべきことがあるという考えに浸るのは、いずれにしても興味深いことです。そして、ここで冷静に見てみると(結局のところ、私はここにいて、家ではありません)、私たちはすべてを理解しているわけではないことを認めざるを得ません。
最初の疑問は、物理をシミュレートするためにどのようなコンピュータを使うのか、ということです。コンピュータ理論は、それが何の違いも生まないという点まで発展しました。汎用コンピュータに到達すれば、それがどのように製造され、実際にどのように作られるかは問題ではなくなります。したがって、私の疑問は、汎用コンピュータで物理をシミュレートできるかどうかです。このコンピュータの要素を局所的に相互接続し、セルオートマトンを例として考えたいと考えています(ただし、無理強いはしません)。しかし、相互作用の局所性に関わる何かを求めています。全体にわたって任意の相互接続を持つ非常に巨大なコンピュータは考えたくないのです。
さて、私たちはどのような物理学を模倣するのでしょうか?まず、古典近似、つまり局所微分方程式で記述されるような物理学のシミュレーションの可能性について説明します。しかし、物理世界は量子力学的であるため、本来の問題は量子物理学のシミュレーションです。私が本当に話したいのはまさにそれなのですが、それについては後で触れます。では、どのようなシミュレーションを私が言っているのでしょうか?もちろん、微分方程式の数値アルゴリズムを設計し、コンピュータを使ってこれらのアルゴリズムを計算し、物理学がどう動作するかを大まかに把握するという、一種の近似シミュレーションがあります。これは興味深いテーマですが、私が話したいのはそれではありません。私が話したいのは、コンピュータが自然と全く同じことを行うという、正確なシミュレーションの可能性についてです。もしこれが証明され、コンピュータの種類が私がすでに説明した通りであれば、有限の空間と時間の中で起こるすべての出来事が、有限回の論理演算で正確に解析可能でなければならない。しかし、現在の物理学の理論はどうやらそうではないようだ。空間は無限に微小な距離まで、波長は無限に大きくなり、項は無限の順序で加算されるなど、様々なことが許されている。したがって、もしこの命題が正しければ、物理法則は間違っていることになる。
そうですね、物理法則をどのように修正できるかという提案がすでにあります。そして、それが私がこの種の問題を研究するのが好きな理由です。例えば、空間は連続的であるという考えを、空間はおそらく単純な格子であり、すべてが離散的(つまり有限の桁数で表せる)であり、時間は不連続にジャンプするという考えに変えることができます。では、それがどのような物理世界になるのか、あるいはどのような計算上の問題を抱えるのかを見てみましょう。例えば、最初に浮かび上がる困難は、光速が方向にわずかに依存すること、そして物理学には実験的に検出できる他の異方性が存在する可能性があるということです。それらは非常に小さな異方性かもしれません。もちろん、物理的な知識は常に不完全であり、現時点での実験よりも優れていて、将来発見されるであろうあるスケールの異方性を予測する何かを設計しようと常に主張することができます。 それは結構です。既知の事実すべてと整合する何かを予測し、私たちが説明していない新しい事実を示唆できれば、それは良い物理学と言えるでしょう。しかし、具体的な例はありません。ですから、私は原理的に異方性があるという事実に反対しているのではなく、どの程度異方性があるかという問題です。もしあなたがそれがこれこれの異方性だと言ったら、私はリチウム原子を使った実験で異方性がそれよりも小さいことを示したこと、そしてあなたのこの理論は不可能であることを話します。
初期に示唆されていたもう一つのことは、自然法則は可逆的であるが、コンピュータのルールはそうではないというものでした。しかし、これは誤りであることが判明しました。コンピュータのルールは可逆的であり、そのことに気づき、発見することは非常に有益なことでした。(編集者注:本論文集に掲載されているベネット、フレドキン、トフォリの論文を参照)。これは、物理学と計算の関係が逆転し、計算の可能性について何かを教えてくれる分野です。ですから、これはコンピュータのルールについて何かを教えてくれるだけでなく、物理学についても何かを教えてくれるかもしれないという点で、興味深いテーマです。
私が望むシミュレーションのルールは、大規模な物理システムをシミュレートするために必要なコンピュータ要素の数は、その物理システムの時空間の体積に比例するだけであるというものです。爆発的な増加は避けたいのです。つまり、これだけの物理現象を説明したい場合、正確に計算でき、一定の大きさのコンピュータが必要になります。もし時空間の体積を倍にするために、指数関数的に大きなコンピュータが必要になるとしたら、それはルールに反すると考えます(ルールを作るのは私であり、そうすることが許されているからです)。では、いくつか興味深い質問から始めましょう。
まず、時間のシミュレーションについてお話ししたいと思います。ここでは、時間は離散的であると仮定します。物理測定の精度は無限ではないので、時間は \(10^{-27}\) 秒未満のスケールで離散的になる可能性があります。(実験との衝突を避けるには、少なくともこの程度にする必要がありますが、必要に応じて \(10^{-41}\) 秒にすることも可能です。そうすれば、私たちのモデルが完成します!)
例えば、タイムウィンセルオートマトンをシミュレートする方法の一つは、「コンピュータが状態から状態へと遷移する」と言うことです。しかし実際には、これは時間の概念を伴う直感的な操作です。つまり、状態から状態へと遷移しているのです。したがって、時間(ちなみに、セルオートマトンの場合の空間と同様に)はまったくシミュレートされておらず、コンピュータ内で模倣されているのです。
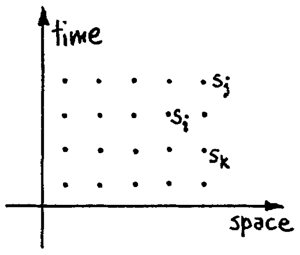
興味深い疑問が浮かびます。「模倣するのではなく、シミュレートする方法はあるのだろうか?」 そうですね、時空観と呼ばれる世界観があります。これは、空間と時間の点が、いわば事前にすべて配置されていると想像するものです。そして、「コンピュータ」のルール(ここでは「コンピュータ」は引用符で囲みます。これは、時間の中で動作する標準的な種類のコンピュータではないためです)は、次のようになります。時空上の各点 \(i\) に状態 \(s_i\) があります。(図1を参照) 時空点 \(i\) における状態 s i は、\(i\) のある近傍にある点 \(j, k\) における状態の与えられた関数 \(F_i(s_j, s_k .... )\) です。 \[ s_i = F_i(s_j, s_k, ... ) \]

この特定の関数が、時刻 \(i\) における関数の値が、時刻 \(i\) よりも前の、時間的に後ろの数点のみに関係するような関数である場合、私が行ったことはセルオートマトンを再記述しただけであることにすぐに気づくでしょう。なぜなら、それは、ある点をそれより前の時刻の点から計算し、次の点を計算し、それを繰り返していくという、特定の順序で処理を進めることができるからです。しかし、より一般的な種類のコンピュータを考えてみましょう。より一般的な関数が存在する可能性があるからです。そこで、時空における点の相互接続の一般性をより広いケースで実現できるかどうかを考えてみましょう。\(F\) が未来と過去の両方の点に依存するとしたら、どうなるでしょうか。それが物理学の仕組みなのかもしれません。現時点での私たちの理論の進め方について触れておきます。多くの物理理論において、数学方程式は、陽電子を時間的に逆方向に移動する電子として、そして物体を前後に結びつける他のものを想像することで、かなり単純化されることが分かっています。重要な疑問は、もしこのコンピュータが設計されたとしたら、実際に解を設計、つまり計算できる組織化されたアルゴリズムが存在するのかということです。関数Fを知っていて、それが未来の変数の関数でもあると仮定します。上記の方程式を自動的に満たすように数値をどのように配置するでしょうか?それは不可能かもしれません。セルオートマトンの場合は可能です。なぜなら、ある行から次の行、さらにその次の行が得られ、それを組織的に行う方法があるからです。関数が、少なくともすぐには、体系的にレイアウトする方法が思いつかないような状況が存在するかどうかは、興味深い問題です。何らかの近似値から考え出す必要があるかもしれませんが、それは興味深い、異なるタイプの計算です。
質問:「これは初期値型の計算とは対照的に、通常の境界値に還元されるのではないですか?」
回答:「はい。ただし、私が説明しているのはコンピュータそのものであることを忘れないでください。」
実際、古典物理学は因果関係があるようです。過去の情報に関して言えば、運動量と位置の両方、あるいは過去の2つの異なる時点における位置(いずれにしても、各時点で2つの情報が必要です)を含めれば、原理的には未来を計算できます。つまり、古典物理学は局所的、因果的、可逆的であり、したがって(既に述べた離散性などを除けば)コンピュータシミュレーションにかなり適応可能であるようです。どうやら、原理的には、それに関して何の問題もありません。
量子力学に目を向けると、ここで得られるのはどうやら確率を予測する能力だけであることがすぐに分かります。私が本当に何を言いたいのか分かってもらえるように、すぐに言っておこうと思いますが、私たちは常に(秘密、秘密、扉を閉めて!)、量子力学が表現する世界観を理解するのに非常に苦労してきました。少なくとも私はそうです。なぜなら、私は十分な年齢なので、まだこのことが自明という段階に達していないからです。ええ、今でも不安になります。そして、そのため、若い学生の中には…ご存知の通り、どんな新しいアイデアも、本当の問題がないことが明らかになるまでに1世代か2世代かかります。私にはまだ本当の問題がないことが明らかになっていません。本当の問題を定義することはできません。ですから、本当の問題はないのではないかと疑っていますが、本当の問題がないと確信しているわけではありません。だからこそ、私は物事を探求するのが好きです。コンピューターについて、量子力学の世界観がどのようなものかという謎があるかもしれないのですが、この疑問を問うことで何か学べるでしょうか?量子力学には確率が関わっているようですが、確率のシミュレーションについてお話ししたいと思います。
確率論、つまり確率を含むものをシミュレートするコンピュータを実現する一つの方法は、確率を計算し、その数値を自然界を表すものとして解釈することです。例えば、ある粒子が時刻 \(t\) に \(x\) に存在する確率が \(P(x, t)\) であるとします。このような確率の典型的な例として、例えば粒子が拡散している場合、次のような微分方程式を満たすことがあります。 \[ \frac{\partial P(x,t)}{\partial t}=-\nabla^2 P(x,t) \] さて、\(t\) と \(x\)、そしておそらく確率そのものも離散化して、この微分方程式を普通の場の方程式を解くのと同じように解き、離散化によって正確な解を得るアルゴリズムを作ることができます。まず、確率の離散化に関する問題があります。\(k\) 桁しか取らないとすると、何かが起こる確率が \(2^{-k}\) より小さい場合、それは全く起こらないと言うことになります。実際にはそうします。何かが起こる確率が \(10^{-700}\) の場合、それは起こらないと言いますが、そうでないことはあまりありません。ですから、そうしても構わないのです。しかし、本当の難しさは次の点にあります。もし、ある系に多数の粒子、例えば \(R\) 個の粒子があるとしたら、ある状況の確率を記述するためには、時刻 \(t\) に点 \(x_1, x_2 ..... x_R\) にこれらの粒子が存在する確率を与える必要があります。これが系の確率の記述となります。したがって、系のあらゆる構成、つまり \(x\) の \(R\) 個の値のあらゆる配置に対して、\(k\) 桁の数値が必要になります。そして、空間に \(N\) 個の点があるとしたら、\(R\) 個の構成が必要になります。実際、空間の各点には電場などの情報が存在するという観点からすると、情報ビットの数が空間の点の数と同じであれば、\(R\) は \(N\) と同じオーダーになります。したがって、確率を求めるには \(N^N\) のような構成を記述する必要があり、コンピュータのサイズが \(N\) のオーダーだとすると、これはコンピュータが保持するには大きすぎます。
ここで強調しておきたいのは、自然の孤立した部分を \(N\) 個の変数で記述するために \(N\) 個の変数からなる一般的な関数が必要であり、コンピュータがこの関数を実際に計算または保存することでこれをシミュレートする場合、自然のサイズを 2 倍 \(N \rightarrow 2N\) にするには、シミュレーションを行うコンピュータのサイズが指数関数的に爆発的に増大する必要があるということです。したがって、前述の規則に従えば、確率を計算することでシミュレーションを行うことは不可能です。
他に方法はあるのでしょうか?どのようなシミュレーションができるのでしょうか?確率理論の配置の確率を計算することは期待できません。しかし、確率的な性質をシミュレートする別の方法(ここでは \(\mathcal{R}\) と呼ぶことにします)は、確率的な性質を、それ自体が確率的なコンピュータ \(\mathcal{C}\) でシミュレートすることかもしれません。このコンピュータでは、すべての数字の最後の2桁を常にランダム化するか、何かひどいことをします。つまり、これは私が確率的コンピュータと呼ぶものになり、出力は入力の一意の関数になります。そして、それを自然現象を模倣するように計算しようとします。つまり、\(\mathcal{C}\) がある状態(初期状態とでも言いましょうか)からある最終状態へ、\(\mathcal{R}\) が対応する初期状態から対応する最終状態へ遷移するのと同じ確率で遷移する、ということです。もちろん、機械をセットアップして自然に任せれば、模倣者は同じことをするわけではなく、同じ確率でしか実行しません。これは良くないのでしょうか? いいえ、問題ありません。その確率がどれくらいなのか、どうやって知るのでしょうか?ご存知のとおり、自然は予測不可能です。コンピューターでそれをどうやって予測できると思いますか?それは不可能です。確率的であれば予測不可能なのです。しかし、確率的システムで実際に行っているのは、自然界での実験を何度も繰り返すことです。コンピュータで同じ実験を何度も繰り返すと(もちろん、自然界で同じことをするのと同じくらいの時間がかかります)、与えられた最終状態の頻度は回数に比例し、自然界で起こるのとほぼ同じ割合(プラスマイナス \(n\) の平方根など)で発生します。言い換えれば、確率的な性質を持つ確率シミュレータを想像し、それで全く満足できると思います。機械は自然界と全く同じことをするわけではありませんが、特定の種類の実験を自然の確率を決定するのに十分な回数繰り返し、コンピュータで対応する実験を行うと、対応する確率が対応する精度(統計と同じ種類の精度)で得られます。
それでは、局所確率コンピュータの特性について考えてみましょう。自然現象を模倣できるかどうか試してみたいからです(ここで言う「自然」とは、量子力学のことです)。その特性の一つは、他のすべての領域での動作を無視するだけで、局所領域での動作を決定できることです。例えば、システム内に世界全体を記述する変数 (\(x_A、x_B\)) があるとします。興味のある変数 (\(x_A\)) は「この辺り」にあり、\(x_B\) は世界全体の結果です。この辺りで何かが起こる確率を知りたい場合は、あらゆる種類の可能性の確率全体を \(x_B\) にわたって積分する必要があります。この確率を計算したとしても、積分は依然として必要です。 \[ P_A(x_A) = \int P(x_A, x_B) dx_B \] これは大変な作業です!しかし、確率を模倣すれば、非常に簡単に実行できます。積分を行うために何もする必要はなく、\(x_B\) の値が何であるかを無視して、領域 \(x_A\) を見るだけです。そして、それゆえ、それは自然の特性を備えています。つまり、局所的であれば、積分したり余分な演算を行ったりするのではなく、他の場所で何が起こっているかを無視するだけで、その領域で何が起こっているかを知ることができます。つまり、演算は一切不要で、何もする必要がないのです。
強調したいもう一つの側面は、方程式が間違いなく次のような形になるということです。空間内の各点 \(i=1,2 .... ,N\) が、小さな状態集合(この集合のサイズは妥当なもの、例えば \(2^5\) まで)から選択された状態 \(s_i\) にあるとします。そして、ある構成 \(\{s_i\}\)(各点 \(i\) における状態 \(s_i\) の値の集合)を見つける確率をある数 \(P(\{s_i\})\) とします。これは、時間の各ジャンプにおいて、 \[ P_{t+1}\left(\{s\}\right)=\sum_{\{s^\prime\}}\left[\prod_i m(s_i|s_j^\prime, s_k^\prime\cdots)\right]P_t(\{s^\prime\}) \] ここで、\(m(s_i|s_j^\prime,s_k^\prime,\cdots)\) は、近傍の値が \(s_j^\prime,s_k^\prime,\cdots,\) であるときに、点 \(i\) で状態 \(s_i\) に遷移する確率です。ここで、\(j, k\) などは \(i\) の近傍にある点です。\(j\) が \(i\) から遠ざかるにつれて、\(m\) は \(s_j^\prime\) の影響を受けにくくなります。各変化において、特定の点 \(i\) の状態は、近傍の状態(点 \(i\) 自身を含むように定義される場合もあります)のみに依存する確率 \(m\) で、以前の状態から状態 \(s\) に遷移します。 これは遷移を行う確率を示します。これはセルオートマトンの場合と同じです。ただ、確定的ではなく、確率です。環境を教えてください。次の瞬間以降、この点が状態 \(s\) にある確率を教えます。これが仕組みです、わかりましたか? つまり、このような形の数式が得られます。
さて、量子力学効果をコンピュータ(万能オートマトンか何か)でどのようにシミュレートできるかという問題に、明確に触れたいと思います。(通常の定式化では、量子力学は関数 \(\psi\) に対するある種の微分方程式を持っています。)単一粒子の場合、\(\psi\) は \(x\) と \(t\) の関数であり、この微分方程式は、先ほどの確率方程式と同じようにシミュレートできます。それで問題ありませんし、単一粒子のシュレーディンガー方程式をシミュレートする小型コンピュータを作っている人もいます。しかし、\(R\) 個の粒子を含む大規模システムの量子力学の完全な記述は、関数 \(\psi(x_1, x_2 ..... x_R, t)\) によって与えられます。この関数は、粒子 \(x_1 ..... x_R\) を見つけるための振幅と呼ばれます。したがって、変数が多すぎるため、\(R\) に比例する要素数、または \(N\) に比例する要素数を持つ通常のコンピュータではシミュレートできません。古典物理学の確率でも同じ問題がありました。したがって、問題は、どのように量子力学をシミュレートするか、ということです。 これには 2 つの方法があります。コンピュータとは何かという従来のルールを放棄し、次のように言うことができます。「コンピュータ自体を、量子力学の法則に従う量子力学要素で構築する」。あるいは、逆にこう言うこともできます。「コンピューターを、私たちが以前考えていたのと同じ種類のもの、つまり論理的で汎用的なオートマトンとして考えてみましょう。この状況を模倣することはできるでしょうか?」ここで私の講演は2つの部分に分かれるので、分けてお話ししたいと思います。
最初の分岐は、いわば余談ですが、「新しい種類のコンピュータ、つまり量子コンピュータでそれができるのか?」というものです(この分岐については後ほど触れます)。私の知る限りでは、量子システム、つまり量子コンピュータの要素集合体でこれをシミュレートできることがわかりました。これはチューリングマシンではなく、別の種類のマシンです。空間の連続性を無視して離散的にするなど、近似的に(古典的なケースと同じように)行えば、様々な場の理論はすべて同じような振る舞いをし、スピンなどの小さな格子構造を使ってあらゆる方法でシミュレートできるというのは確かに真実のようです。場の理論の現象(世界が離散格子でできている場合)は、固体理論(結晶原子の格子構造の解析に過ぎず、固体の場合、各原子は量子力学の法則に従って番号が付けられた単なる点である)の多くの現象によってよく模倣できることが、繰り返し指摘されてきました。例えば、スピン格子内のスピン波は、場の理論におけるボーズ粒子を模倣します。したがって、適切な種類の量子マシンを用いれば、物理世界を含むあらゆる量子系を模倣できるというのは真実であると私は信じています。しかし、量子システムの相互シミュレーションに関する一般理論がこれまでに解明されたことがあるのかどうかは分かりません。そこで、もう一つの興味深い問題として、古典コンピュータの場合のように、実際に相互シミュレーション可能な、つまり等価な、異なる種類の量子力学システムのクラスを解明することを提案します。何でもできる一種の汎用コンピュータが存在し、それがどのように設計されているかは特に問題にならないことが分かっています。同様に、どのような種類の量子力学システムが相互にシミュレーション可能かを調べ、すべてをシミュレーションできる特定のクラス、あるいはそのクラスの特性を見つけ出す必要があります。言い換えれば、汎用量子シミュレータとは何でしょうか?(空間と時間の離散化を前提とした場合)。もし離散量子系があるとしたら、他にどのような離散量子系がそれを正確に模倣しているのでしょうか?そして、すべての系に匹敵するクラスはあるのでしょうか?この質問に答え、クラスを見つけるのは比較的簡単だと思いますが、まだ試していません。
次のような推測を試してみよう。あらゆる有限量子力学系は、時空上の各点において二つの基本状態しか持たないような別の系を仮定することによって、正確に記述でき、正確に模倣できる、という推測である。その点は占有されているか、空であるかのどちらかであり、これらが二つの状態である。その点に関連する量子力学演算子の数学は非常に単純であろう。 \[ \begin{align} a =消滅 &= \begin{array}{c|c l} & 占有 & 非占有 \\ \hline 占有 & 0 & 0 = \frac{1}{2}(\sigma_x-i\sigma_y) \\ 非占有 & 1 & 0 \end{array} \\ \\ a^* = 生成 &= \begin{array}{c|c l} & & \\ \hline & 0 & 1 =\frac{1}{2}(\sigma_x+i\sigma_y) \\ & 0 & 0 \end{array} \\ \\ n = 数 &= \begin{array}{c|c l} & & \\ \hline & 1 & 0 = a^*a=\frac{1}{2}(1+\sigma_z) \\ & 0 & 0 \end{array} \\ \\ \mathbb{1}=恒等式 &= \begin{array}{c|c l} & & \\ \hline & 1 & 0 \\ & 0 & 1 \end{array} \end{align} \]
点が占有されている場合、それを消滅させる演算子 \(a\) があります。つまり、点を空に変えるのです。共役演算子 \(a^*\) は逆の動作をします。空の場合は、それを占有します。もう一つの演算子 \(n\) は、数と呼ばれ、「そこに何かがあるか?」と尋ねるものです。小さな行列が、それが何をするかを示しています。もしそこに何かがあれば、\(n\) は \(1\) を取得してそのままにしておきます。そうでなければ、何も起こりません。実際、これは他の 2 つの積と数学的に等価です。そして、恒等式 \(\mathbb{1}\) があります。これは、数学を完成させるために必ずここに入れなければなりませんが、実際には何の役にも立ちません!
ちなみに、上記の式の右辺では、同じ演算子が行列で書かれていますが、これは多くの物理学者にとってより便利だと考えられています。なぜなら、エルミート行列であるため、物理学者にとって扱いやすいからです。彼らはパウリ \(\sigma\) 行列という別の行列を発明しました。 \[ \sigma_z= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} , \sigma_x= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} , \sigma_y= \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} , \mathbb{1}= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \] これらはスピン、つまりスピン1/2と呼ばれています。つまり、スピン1/2格子について話していると言われることもあります。
問題は、これらの演算子のみを含むハミルトニアンを、他の時空点上の対応する演算子と局所的に結合したものを書いた場合、離散的で有限の自由度を持つあらゆる量子力学系を模倣できるかどうかです。ボーズ粒子を含むあらゆる量子力学系に対して、ほぼ確実にそれが可能であることは分かっています。フェルミ粒子がそのような系で記述できるかどうかは分かりません。ですから、この点については未定としておきます。まあ、これは私が汎用量子力学シミュレーターと呼んでいたものの一例ですが、フェルミ粒子を扱えるかどうか確信が持てないので、十分かどうかは分かりません。
さて、次に提起したい疑問は、もちろん興味深いものです。つまり、「量子系は古典的な(おそらく確率的でしょうが)汎用コンピュータによって確率的にシミュレートできるのか?」ということです。言い換えれば、量子系と同じ確率を与えるコンピュータのことです。もし、私がこれまで説明してきた古典的なコンピュータ(前のセクションで説明した量子コンピュータではなく)をコンピュータとして、いかなる法則も変更されておらず、ごまかしもなければ、答えは間違いなく「ノー」です!これは「隠れた変数問題」と呼ばれます。つまり、量子力学の結果を古典的な汎用装置で表現することは不可能なのです。この問題について少し理解するために、量子方程式を可能な限り古典的な方程式に近い形で表してみましょう。そうすれば、何が困難で、何が起こるのかが分かります。まず第一に、通常の方法では \(\psi\) をシミュレートできません。既に説明したように、変数が多すぎるからです。唯一の望みは確率をシミュレートすることです。つまり、量子力学システムによって計算された自然界で観測されるのと同じ確率で、コンピュータに何かをさせるということです。セルオートマトンか何かで、自然界と同じ確率で模倣できますか?量子力学が正しいと仮定して、あるいは少なくとも空間と時間を離散化した後では正しいと仮定して、それができるかどうか試してみましょう。ここで指摘しておかなければならないのは、正しい量子確率を使って、確率、つまり結果を直接生成する必要があるということです。直接的にというのは、すべての数値を保存する方法がないため、現象を直接模倣するしかないのです。
すると、波動関数ではなく、密度行列と呼ばれるものが、この計算にははるかに有用であることがわかります。これは、\(\psi\) の方程式よりも複雑なので、数式としてはあまり有用ではありませんが、ここでは数学的な複雑さや、どの計算方法が最も簡単かについては気にしません。なぜなら、コンピュータを使えば、最も簡単な方法で計算するためにそれほど注意する必要がないからです。そこで、方程式の複雑さがわずかに増す(それほど大きくは増えませんが)ので、密度行列に目を向けます。これは、純粋な波動関数 \(\psi(x)\) の状態にある座標 \(x\) の単一粒子に対して、次のようになります。 \[ \rho(x, x^\prime)=\psi^*(x)\psi(x^\prime) \] これには、2つの座標 \(x, x^\prime\) の関数という特殊な性質があります。各座標に関連付けられた2つの量 \(x\) と \(x^\prime\) の存在は、古典力学において状態を記述するために \(x\) と \(\dot{x}\) という2つの変数が必要であるという事実に似ています。状態は2つの情報(「位置」と「速度」)を持つ2次の装置によって記述されます。したがって、配置を記述するためには、古典力学の場合と同様に、粒子に関連付けられた2つの情報が必要です。(ここでは1つの粒子の密度行列を記述しましたが、もちろん、\(R\) 個の粒子についても同様のものがあり、\(2R\) 個の変数の関数です)。
この量は確率の数学的性質の多くを持ちます。 例えば、状態 \(\psi(x)\) が不確実であるが、確率 \(p_\alpha\) で \(\psi_\alpha\) である場合、密度行列は各状態 \(\alpha\) について行列の適切な重み付き和となります。 \[ \rho(x, x^\prime)=\sum_\alpha p_\alpha \psi_\alpha^*(x)\psi_\alpha(x^\prime) \] 古典的な確率にさらに似た性質を持つ量は、ウィグナー関数です。これは密度行列の単純な再表現です。 単一粒子の場合 \[ W(x, p)=\int \rho\left(x+\frac{y}{2}, x-\frac{y}{2}\right)e^{ipy}dy \] ここでは両者の類似性を強調するため、ウィグナー関数ではなく引用符で囲んで「確率」と呼ぶことにします。これらの引用符に注意して、引用符がない場合は真の確率を意味します。「確率」が確率のすべての数学的性質を備えているとすれば、引用符を削除してシミュレーションすることができます。\(W(x, p)\) は、粒子が位置 \(x\) と運動量 \(p\) を持つ「確率」です(\(dx\) と \(dp\) に基づきます)。これは通常の確率と類似したどのような性質を持っていますか?
この式には、変数が多く、有限領域に関連する「確率」を知りたい場合、他の変数は(積分によって)無視できるという性質があります。さらに、\(x\) で粒子が見つかる確率は \(\int W(x,p)dp\) です。\(W\) を \(x\) と \(p\) が見つかる確率と解釈できるなら、これは期待される式になります。同様に、\(p\) の確率は \(\int W(x, p)dx\) であると期待されます。これら2つの式は正しいので、\(W(x, p)\) が \(x\) と \(p\) が見つかる確率である可能性が期待できます。そこで問題となるのは、この \(W\) をシミュレートする装置を作れるかどうかです。そうすれば、問題なく動作するはずです。
私が注目した量子系はスピン1/2(占有と非占有、あるいはスピン1/2は同じ意味)で最もよく表現できたので、スピン1/2の物体に対しても同じことを試みたところ、かなり簡単にできました。以前は1つの物体に占有と非占有の2つの状態しかありませんでしたが、完全な記述(時間の関数として物事を展開するため)には2倍の変数が必要になり、それは各点に占有または非占有の2つのスロット(以下、+と-で示す)が必要になり、\(x\) と \(\dot{x}\)、あるいは \(x\) と \(p\) に類似しています。つまり、4つの数字、4つの「確率」\(\{f_{++}, f_{+-}, f_{-+}, f_{--}\}\) が見つかります。これらは、両方の記号が上、1つが上、1つが下、といった状態にあるものを見つける確率と全く同じように振る舞います。なぜ全く同じではないのか説明が必要ですが、同じように振る舞います。例えば、4つの「確率」の合計 \(f_{++}+f_{+-}+ f_{-+}+f_{--}\) は 1 です。量子システムでは 1 つしかなかったのに、1つの物体には2つの添え字、つまり各点に2つの 1 と 0 があることになります。例えば、最初の添え字が正かどうかを知りたい場合、その確率は \[ Prob(\text{最初の添え字が+}) = f_{++} + f_{+-} [\text{スピンz アップ }] \] つまり、2番目の添え字は気にしなくていい。最初の添え字が負である確率は \[ Prob(\text{最初の添え字がー}) = f_{-+}+ f_{--} [\text{スピンz ダウン}] \] これら2つの式は量子力学において全く正しいです。「確率」\(f\)が本当に引用符なしの確率であるかどうかについては、私は曖昧な表現をしています。しかし、左辺に引用符なしの確率を書くときは、曖昧な表現ではありません。それはまさに量子力学的な確率です。ここでは完全に正しく解釈されています。同様に、2番目の添え字が正である確率は、次のように求められます。 \[ Prob(\text{二番目の添え字が+}) =f_{++}+f_{-+} [\text{スピンx アップ}] \] そして同様に \[ Prob(\text{二番目の添え字が-}) = f_{+-}+ f_{--} [\text{スピンx ダウン}] \]
システムについて他の質問をすることもできます。「両方の指数が正である確率はどれくらいか?」と知りたいかもしれません。これは面倒なことになります。しかし、面倒なことはなく、正しい物理的答えが得られる他の質問をすることもできます。例えば、「2つの指数が同じである確率はどれくらいか?」と尋ねることができます。それは \[ Prob(1番目と2番目の添え字が一致) = f_{++} + f_{--} [\text{スピンy アップ}] \] あるいは、添え字が一致しない、あるいは異なるという確率、 \[ Prob(1番目と2番目の添え字不一致) = f_{+-}+ f_{-+} [\text{スピンy ダウン}] \] すべて完璧です。これらの確率はすべて正しく、意味を成しており、上記の角括弧で示したスピンモデルにおいて正確な意味を持ちます。他にも「確率」の組み合わせ、つまりこれらのfの線形結合があり、それらも物理的に意味のある確率を生み出しますが、今はそれについては触れません。他にも質問できる線形結合はありますが、個々の\(f\)について質問することはできないようです。
さて、格子上の多数の相互作用スピンに対して、相関関係にある可能性の「確率」を与えることができます(引用符は、それが確率であるかどうかについてはまだ疑問が残ることを思い出させます)。 \[ F(s_1,s_2,\cdots,s_N) (s_i \in \{++,+-,-+,--\}) \] 次に、\(F\) が時間とともにどのように変化するかを示す量子力学方程式を探すと、それはまさに古典理論について上で書いた形と全く同じです。 \[ F_{t+1}(\{s\})=\sum_{\{s^\prime\}}\left[\prod_i M(s_i|s_j^\prime,s_k^\prime,\cdots)\right]F_t(\{s^\prime\}) \] しかし、今度は \(P\) の代わりに \(F\) が使われます。\(M(s_i|s_j^\prime,s_k^\prime,\cdots)\) は、隣接ノードが \(s^\prime\) 配置にあるときに、\(i\) の状態が\(s_i\)に変化する単位時間あたり、またはタイムジャンプあたりの「確率」として解釈されるようです。もしそのような確率\(M\)を考案できれば、通常の論理に従ってその方程式を書きます。それらは正しい方程式であり、この\(F\)に対する真の、正しい、量子力学的な方程式です。したがって、「よし、確率コンピュータでこれを模倣できる!」と言えるでしょう。
一つだけ間違っている点があります。残念ながら、これらの方程式はいわゆる「確率」に基づいて解釈することはできません。あるいは、この確率論的コンピュータではシミュレーションできません。なぜなら、\(F\) は必ずしも正ではないからです。 時には負になることもあります!ある状態から別の状態に移行する(いわゆる)「確率」である \(M\) 自体が正ではありません。単一の物体について \(f\) まで遡って考えてみると、これも必ずしも正ではありません。
ここでの可能性の例としては \[ f_{++}=0.6 f_{+-}=-0.1 f_{-+}=0.3 f_{--}=0.2 \]
\(f_{++}+f_{+-}\) の合計は 0.5 で、最初の指数が正になる確率は 50% です。最初の指数が負になる確率は \(f_{-+}+f_{--}\) の合計で、これも 50% です。2 番目の指数が正になる確率は \(f_{++}+ f_{-+}\) の合計で 9/10 です。負になる確率は \(f_{+-}+ f_{--}\) で 1/10 です。つまり、プラスかマイナスかのどちらかです。一致する確率は 8/10 で、一致しない確率はプラス 2/10 です。つまり、すべての物理的な確率はプラスになります。しかし、元々の\(f\)は正ではなく、そこに大きな難しさがあります。確率論的な古典世界と量子世界の方程式の唯一の違いは、どういうわけか確率が負になるように見えることと、私の知る限りではシミュレーションの方法がわからないことです。さて、これが根本的な問題です。答えはわかりませんが、古典的な確率論的コンピュータで模倣できるものにできるだけ近づけようと努力すると、問題が発生することを説明したいと思いました。
なぜこのようなマイナス記号が避けられないのか、あるいは少なくとも何らかの困難を抱えているのかを説明したいと思います。皆さんはおそらくアインシュタイン・ポドルスキー・ローゼンのパラドックスの例を聞いたことがあるでしょうが、ここでは量子論が予測する答えを実際に与えてくれる、実際に実行可能な物理実験の小さな例を説明します。そしてその答えは確かに正しく、実験を行えば間違いなく得られます。ここでは光子の偏光の例を使います。これは二状態システムの例です。光子が来ると、X偏光かY偏光のどちらかであると言えます。それを調べるには方解石を入れます。光子は方解石を通過して、どちらかの方向に、実際にはわずかに離れている方向に出ていきます。そして鏡をいくつか入れますが、それは重要ではありません。 2本のビーム、つまり光子が到達できる2つの場所が得られます。(図2参照)
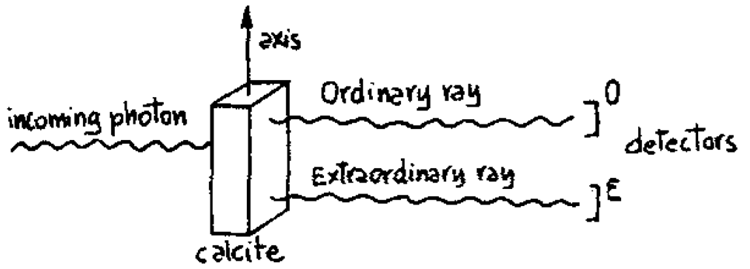
偏光した光子を入射すると、それは常光線と呼ばれる一方の光線、あるいは異常光線と呼ばれるもう一方の光線に入射します。そこに検出器を設置すると、入射した光子は必ずどちらか一方に100%出射し、半々ではありません。どちらか一方に光子が見つかるのです。常光線で光子が見つかる確率と異常光線で光子が見つかる確率を足すと常に1になります。この法則は成り立ちます。さらに、両方の検出器で光子が見つかることはありません。(もし2つの光子を入射すれば、その光子も検出できるかもしれませんが、その場合は強度を下げます。これは技術的な問題で、両方の検出器で光子が見つかるわけではありません。)
さて、次の実験は、4つの偏光ビームへの分離です(図3参照)。2つの方解石を、それぞれの軸が相対角度\(\phi\)を持つように一列に並べます。2つ目の方解石はたまたま2つの位置で描いていますが、同じ方解石を使うかどうかは関係ありません。片方の方解石から出た常光線をもう片方の方解石に通して、その常光線(ここでは常-常光線 (\(O-O\)) と呼びます)を観察します。もう片方の異常光線(ここでは常-異常光線 (\(O- E\)) と呼びます)を観察します。そして、最初の方解石から出た異常光線は\(E-O\) 光線として出ます。そして、\(E-E\) 光線も出てきます。さて、何が起こるか、考えてみましょう。
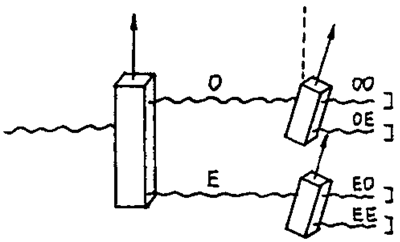
次のようなことがわかります。光子が入ってくると、常に4つのカウンターのうち1つだけが作動します。
光子が最初の方解石から \(O\) の場合、2番目の方解石は確率 \(\cos^2\phi\) で \(O-O\) を、または相補確率 \(1-\cos^{-1}\phi=\sin^2\phi\) で \(O-E\) を生じます。同様に、\(E\) 光子は確率 \(\sin^2\phi\) で \(E-O\) を、または確率 \(\cos^2\phi\) で \(E-E\) を生じます。
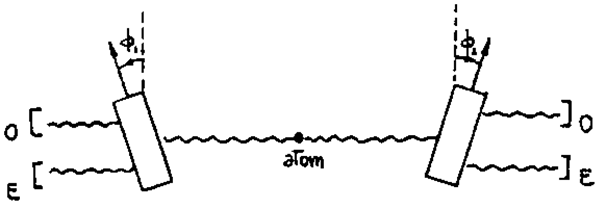
起こり得るのは、原子が2つの光子を反対方向に放出することです(例えば、\(H\) 原子における\(3s\rightarrow 2p \rightarrow 1s\) 遷移)。これらの光子は、垂直方向に \(\phi_1\) と \(\phi_2\) に置かれた2つの方解石を通して、(あなたと私が)同時に観測されます。量子論と実験は、私たち2人が通常の光子を検出する確率 \(P_{OO}\) が \[ P_{OO} = \frac{1}{2} \cos^2 (\phi_2 - \phi_1) \] 我々が異常光線を観測する確率 \(P_{EE}\) は同じである \[ P_{EE} = \frac{1}{2}\cos^2(\phi_2 - \phi_1) \] 私が \(O\) を見つけ、あなたが \(E\) を見つける確率 \(P_{OE}\) は \[ P_{OE} = \frac{1}{2}\sin^2(\phi_2 - \phi_1) \]
そして最後に、私が \(E\) を測定し、あなたが \(O\) を測定する確率 \(P_{EO}\) は \[ P_{EO} = \frac{1}{2} \sin^2(\phi_2 - \phi_1) \] あなた自身の測定から、私が \(O\) または \(E\) のどちらを得るかは常に予測できることに注意してください。私が選んだ任意の軸 \(\phi_1\) に対して、あなたの軸 \(\phi_2\) を \(\phi_1\) に設定してください。 \[ P_{OE}= P_{EO} = 0 \] そしてあなたが得るものは何でも私も得なければなりません。
局所確率コンピュータではどうなるか見てみましょう。光子 1 は、確率 \(f_\alpha(\phi_1)\) で何らかの条件 \(\alpha\) にある必要があり、その条件 \(\alpha\) は光子 1 が通常の光線として通過することを決定します[\(E\)として通過する確率は\(1-f_\alpha(\phi_1)\)です]。同様に、光子 2 は確率 \(g_\beta(\phi_2)\) で条件 \(\beta\) にあります。\(p_{\alpha\beta}\) が条件ペア \(\alpha, \beta,\) を見つけるための結合確率であるとすると、両者が \(O\) 光線を観測する確率 \(P_{OO}\) は \[ P_{OO}(\phi_1, \phi2) = \sum_{\alpha\beta} p_{\alpha\beta}f_\alpha(\phi_1)g_\beta(\phi_2) \sum_{\alpha\beta} p_{\alpha\beta} = 1 \] 同じく \[ P_{OE}(\phi_1, \phi_2) = \sum_{\alpha\beta} p_{\alpha\beta}\left(1-f_\alpha(\phi_1)\right)g_\beta(\phi_2) etc. \] 条件 \(\alpha\) は光子の進路を決定します。条件には何らかの相関関係があります。このような式では、\(p_{\alpha\beta}, f_\alpha(\phi_1), g_\beta(\phi_2)\)が実確率(つまりすべて正)である場合、上記の量子結果を再現することはできません。ただし、それらが「確率」である場合、つまり条件や角度によっては負になる場合は簡単です。なぜそうなるのかを分析しましょう。
どのような条件なのかは分かりませんが、どんな条件でも、どの方向においても異常光か通常光かの確率 \(f_\alpha(\phi)\) は 1 か 0 でなければなりません。そうでなければ、反対側を予測することはできません。光子がここに来るたびに、どの方向に進むかが絶対的に決まっていない限り、私が何を得るのかを確実に予測することはできません。したがって、光子がどのような条件にあっても、それが通常光か異常光かを決定する何らかの隠れた内部変数が存在します。この決定は確率的ではなく決定論的に行われます。そうでなければ、私が何を得るのかを正確に予測できたという事実を説明できません。では、このようなことが起こると仮定してみましょう。\(30^\circ\) の倍数の角度についてのみ結果を議論するとします。
それぞれの図(図5)には、角度 \(0^\circ, 30^\circ, 60^\circ, 90^\circ, 120^\circ\)、\(150^\circ\) が示されています。粒子が私のところに現れ、何らかの状態にあるとします。そのため、\(0^\circ\)、\(30^\circ\) などでどのような状態になるかはすべて、状態によって予測(決定)されます。例えば、ある特定の状態において、\(0^\circ\) の場合は異常状態(黒点)、\(30^\circ\) の場合は異常状態、\(60^\circ\) の場合は通常状態(白点)、といった予測が立てられているとします(図5a)。ちなみに、結果は90度では互いに補完関係にあります。なぜなら、光線は常に異常光線か普通光線のどちらかであることを覚えておいてください。ですから、90度回転させると、普通光線だったものが異常光線になります。したがって、どのような状態であっても、ある種の予測パターンがあり、普通光線か異常光線かのどちらか、つまり3と3のどちらかを予測できます。なぜなら、直角では同じ色ではないからです。同様に、分離したときにあなたのところに来る粒子も同じパターンを持っているはずです。なぜなら、あなたの粒子を測定することで、私が何を得るかを判断できるからです。どのような状況で結果が出ても、パターンは同じでなければなりません。ですから、60度で白になるのか知りたい場合、 \(60^\circ\) で測定すれば白が見つかるでしょう。したがって、あなたは私の場合は白、つまり普通だと予測するでしょう。さて、実験するたびにパターンは同じではないかもしれません。光子対を作るたびにこの実験を何度も繰り返しますが、図 5a と同じになる必要はありません。次の実験では、図 5c のように、私の光子が各角度で \(O\) または \(E\) になると仮定しましょう。すると、あなたのパターンは図 5d のようになります。しかし、それが何であれ、あなたのパターンは私のパターンと全く同じでなければなりません。そうでなければ、対応する角度を測定しても、私が何を得るかを正確に予測することはできません。以下同様に続きます。実験するたびに、異なるパターンが得られます。簡単です。6つの点があり、そのうち3つは白です。それらを様々な方法で追跡すれば、何が起こるかわかりません。同じ角度で測定すれば、常に同じ結果が得られます。
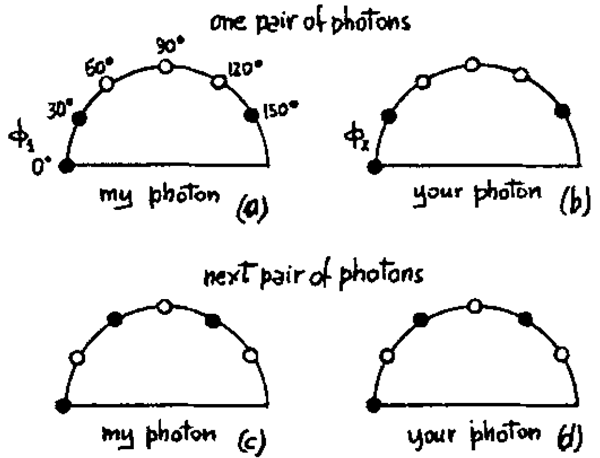
さて、\(\phi_2 - \phi_1= 30^\circ\) で測定すると仮定します。そして、どれくらいの確率で同じ結果が得られるでしょうか。まずはこの例 (図 5a、5b) を試してみましょう。両方とも白、あるいは両方とも黒という同じ結果になる確率はどれくらいでしょうか。結果は次のようになります。私が「それらが出てきた後、ランダムに方向を選びます。その方向の右に \(30^\circ\) を測定するように指示します。すると、私が何を得たとしても、隣の目が異なれば、あなたは違う結果を得ます。(隣の目が同じであれば、同じ結果になります。) あなたが私と同じ結果になる確率はどれくらいでしょうか。確率とは、隣の目が同じ色である回数です。少し考えれば、図 5a の場合、3 分の 2 の確率で同じ色であることがわかります。最悪のケースは黒/白/黒/白/黒/白で、一致確率はゼロになります(図5c、d)。8つの異なるケースすべてを検討すると、最大の答えは3分の2であることがわかります。このような古典的な方法では、\(30^\circ\)での一致確率が3分の2より大きくなるように設定することはできません。しかし、量子力学の式は\(cos^2 30^\circ\)(つまり3/4)を予測し、実験もこれと一致しています。そして、そこに難しさがあります。
それが全てです。それが難しいのです。だからこそ、量子力学は局所古典コンピュータでは模倣できないようです。
私はいつも、量子力学の難しさをどんどん小さな領域に押し込めて、この特定の事柄についてますます心配するようにしてきました。あるものが他のものより大きいという数値的な問題に押し込められるなんて、ほとんど馬鹿げているように思えます。しかし、それが現実です。この種の論理があれば、どんな論理的議論も導き出せないほど大きな問題なのです。さて、「この種の論理」と言いますが、他にどんな可能性があるでしょうか?可能性がないかもしれませんが、もしかしたらあるかもしれません。可能性について議論してみるのは興味深いことです。私は時間の可能性について少し触れました。物事は過去だけでなく未来にも影響を受ける可能性があり、したがって私たちの確率はある意味で「錯覚的」であるということです。私たちは過去の情報しか持っておらず、次のステップを予測しようとしますが、実際にはそれは私たちが到達できない近い未来に依存している、といったようなものです。非常に興味深い疑問は、量子力学における確率の起源です。別の言い方をすれば、私たちは好きな実験を何でもできるという幻想を抱いています。しかし、私たちは皆同じ宇宙から生まれ、宇宙と共に進化してきたため、実際には「真の」自由などありません。なぜなら、私たちは特定の法則に従い、特定の過去から来ているからです。私たちが行う実験と何らかの形で相関関係にあるため、見かけ上の確率は、ランダムであると仮定した場合、本来あるべき姿とは異なって見えるのでしょうか。このような疑問は多種多様にありますが、私が試みているのは、コンピューターシミュレーションの可能性について考えている皆さんに、この問題に十分な注意を払い、量子力学の真の答えを可能な限り理解し、物理学者がこれを説明するために考え出さざるを得なかった視点とは異なる視点を、皆さんが考え出せるかどうかを検討してもらうことです。実際、物理学者たちは良い視点を持っていない。誰かが多世界描像について何か呟いたが、その多世界描像によれば波動関数\(\psi\)こそが実在するもので、\(N^R\)のような変数がそんなにたくさんあるなら魚雷なんてどうでもいい、ということになる。これらすべての異なる世界、あらゆる配置の配置は、私たちの配置の配置と同じように存在していて、私たちはたまたまこの世界の中にいるだけだ。可能性はあるが、私はあまり納得していない。
ですから、何か別の解決策があるのではないかと考え、ここでこの問題を強調、あるいは提起したいのです。なぜなら、コンピュータの発見とコンピュータに関する思考は、人間の推論の多くの分野で非常に役立つことが分かってきたからです。例えば、言語を理解できるコンピュータを作ろうとするまでは、言語に対する理解、文法理論などがどれほど不十分であったかを、私たちは本当に理解していませんでした。コンピュータの仕組みを理解しようとすることで、心理学について多くのことを学ぼうとしました。推論、関係性、観察、測定などに関する興味深い哲学的問題があり、コンピュータは私たちに新しいタイプの思考で新たな思考を促しました。そして私がしていたのは、コンピュータ型の思考が、もし本当に必要なら、何か新しいアイデアを与えてくれることを期待していただけです。どうでしょう、もしかしたら物理学は今のままで全く問題ないのかもしれません。フレドキンが常に推し進めている、物理学のコンピュータシミュレーションを見つけようとするプログラムは、私にとっては実行に移すべき素晴らしいプログラムに思えます。 彼と私は素晴らしく、熱く、果てしない議論を重ねてきましたが、私の主張は常に、その真の用途は量子力学にあるというものでした。 したがって、量子力学的現象、つまり量子力学的現象を説明するという難題に十分な注意を払い、受け入れる必要があるのです。 したがって、状況を分析する際には、これらの現象をしっかりと理解する必要があります。 そして、私は古典理論だけに頼った分析には満足していません。なぜなら、自然は古典的ではないからです。 自然のシミュレーションを作りたいのであれば、量子力学的にすべきです。そして、これは実に素晴らしい問題です。 なぜなら、それほど簡単そうには見えないからです。ありがとうございます。
質問:解釈のために補足すると、まずAがBを与えられた場合の確率と、AとBが同時に起こる確率(つまり、一方の観察者が結果を見て、もう一方の観察者に確率を割り当てる確率)についてお話しになりました。そして次に、量子力学的な結果が3/4で、これが2/3であるというパラドックスについて言及されました。これらは本当に同じ確率なのでしょうか?一方は同時確率で、もう一方は条件付き確率ではないでしょうか?
答え: いいえ、同じです。\(P_{OO}\) はあなたと私が通常光線を観測する同時確率で、\(P_{EE}\) は2つの異常光線の同時確率です。私たちの観測結果が一致する確率は \[ P_{OO} + P_{EE} = \cos^2 30^\circ = 3/4 \]
質問:それはある意味で、光子から、あるいは粒子からどれだけの情報が得られるかという仮定に依存しているのでしょうか?そして次に、予測についてのあなたの質問、つまり予測についてのあなたのコメントは、ある意味で哲学的な問いを彷彿とさせます。「自由意志や予定説が存在するかどうかという問いには、何か意味があるのでしょうか?」 つまり、観察者と実験の相関関係、そして「予測を観察者に報告できるようなテストを構築することは可能か、それとも、情報を表現する能力はすでに使い果たされているのか?」という疑問です。そして、あなたはすでにすべての情報を使い果たしていて、予測は理論の範囲外にあるのではないかと私は考えています。
答え:こうしたことはすべて理解できません。深遠な疑問、重大すぎる疑問です。しかし物理学者は、こうした疑問をすべて回避する、ある種の愚かな方法を持っています。彼らはただこう言います。「いいかい、君はカウンターを2つ取って、方解石の横に置いて、この物質が何回出てくるか数えてみると、75%の確率で出てくる」。そしてこう言います。「では、同じ結果を生み出し、局所的に動作する装置でこれを真似できるだろうか?」と。そして、それを実現する何らかの方法を発明しようと試みます。そして、通常の考え方でやろうとすると、同じ確率でそこに到達できないことに気づきます。したがって、何らかの新しい考え方が必要なのですが、物理学者は頭が鈍いので、自然しか見ず、こうした新しい考え方を知らないのです。
質問:講演の冒頭で、物理学の真の計算を行うために、様々なものを離散化することについてお話されていました。しかし、空間と時間、そしてある場所に存在する可能性のある確率、エネルギー、あるいはある場の値などには、いくつかの違いがあるように思えます。空間と時間の量子化や離散化と、存在する可能性のある特定のパラメータや値の離散化を区別する理由はあるでしょうか?
回答:いくつかコメントしたいと思います。量子化か離散化かとおっしゃいましたが、それは非常に危険です。量子論と量子化は非常に特殊な種類の理論です。離散化という言葉が適切です。量子化は別の種類の数学です。離散化について話す場合、もちろん物理法則を変えなければならないと指摘しました。なぜなら、現在書かれている物理法則は、古典的な極限では、空間と時間のどこにでも連続変数を持っているからです。例えば、あなたの理論で電場を使うとしたら、電場は(有限個の要素で模倣、計算可能であれば)無限の数の可能な値を持つことはできません。デジタル化する必要があります。電場を使わずに物事を記述し直すことで理論をうまくやり過ごせるかもしれませんが、仮にそれが不可能だと気づき、電場を使って記述しようとしたとしましょう。すると、例えば、電場が一定量より小さい場合、電場は全く存在しない、などと言わざるを得なくなります。これらは非常に興味深い問題ですが、残念ながら古典物理学には向きません。なぜなら、例えば100光年離れた星が波を起こして地球にやってくるとします。そして、それがどんどん弱くなっていきます。電場はどんどん弱くなっていきます。どれほど低い値まで測定できるでしょうか?カウンターを置くと、「カチッ」という音がして、しばらく何も起こりません。「カチッ」という音がして、しばらく何も起こりません。全く離散化されていません。そんな小さな場を測定することは不可能ですし、小さな場を見つけることもできませんし、そんな小さな場を模倣する必要もありません。なぜなら、模倣しようとしている世界、つまり物理世界は古典世界ではなく、異なる振る舞いをするからです。ですから、電場を離散化するという具体的な例は、物理学者としては根本的に難しい問題だとは思いません。なぜなら、それは単に場があまりにも小さくなりすぎて、量子力学を使った方がよいということであり、つまり間違った方程式を解いていて、間違った問題を解いているということになるからです!私ならこう答えます。なぜなら、電場が「1」か何かから出ていると想像すると、最低でも1つしか得られませんが、私たちが見ているのは完全な光子だからです。これらすべては、物理世界が離散的な方法で表現可能であるというのは、どういうわけか真実であることを示唆しています。なぜなら、このような窮地に陥るたびに、この実験は、電場がゼロになった場合に生じる問題、つまり、電場が世界が扱える桁数を下回ってしまうために、ある距離を超える星が見えなくなってしまう問題を回避するために必要なことだけを行っていることが分かるからです。